Snub tetraoctagonal tiling

In today's world, Snub tetraoctagonal tiling has taken a leading role in society, generating a significant impact in different areas of daily life. Since its emergence, Snub tetraoctagonal tiling has generated endless debates, criticisms, and reflections, becoming a topic of interest for different sectors and disciplines. Its influence has transcended borders and has become a fundamental part in decision-making, in the construction of identity, in the development of technology, and in the creation of new forms of communication. In this article, we will explore the many facets of Snub tetraoctagonal tiling and its relevance in contemporary society.

Snub tetraoctagonal tiling
Snub tetraoctagonal tiling
Poincaré disk model of the hyperbolic plane
Type Hyperbolic uniform tiling
Vertex configuration 3.3.4.3.8
Schläfli symbol sr{8,4} or
Wythoff symbol | 8 4 2
Coxeter diagram
Symmetry group +, (842)
Dual Order-8-4 floret pentagonal tiling
Properties Vertex-transitive Chiral

In geometry, the snub tetraoctagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of sr{8,4}.

Images

Drawn in chiral pairs, with edges missing between black triangles:

The snub tetraoctagonal tiling is seventh in a series of snub polyhedra and tilings with vertex figure 3.3.4.3.n.

4n2 symmetry mutations of snub tilings: 3.3.4.3.n
Symmetry
4n2 		Spherical Euclidean Compact hyperbolic Paracomp.
242 342 442 542 642 742 842 ∞42
Snub
figures
Config. 3.3.4.3.2 3.3.4.3.3 3.3.4.3.4 3.3.4.3.5 3.3.4.3.6 3.3.4.3.7 3.3.4.3.8 3.3.4.3.∞
Gyro
figures
Config. V3.3.4.3.2 V3.3.4.3.3 V3.3.4.3.4 V3.3.4.3.5 V3.3.4.3.6 V3.3.4.3.7 V3.3.4.3.8 V3.3.4.3.∞
Uniform octagonal/square tilings
, (*842)
(with (*882), (*444) , (*4222) index 2 subsymmetries)
(And (*4242) index 4 subsymmetry)

=

=
=
=
=
=

=

=

=
=


=
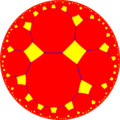
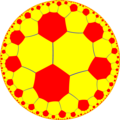
{8,4} t{8,4}
 r{8,4} 2t{8,4}=t{4,8} 2r{8,4}={4,8} rr{8,4} tr{8,4}
Uniform duals
V84 V4.16.16 V(4.8)2 V8.8.8 V48 V4.4.4.8 V4.8.16
Alternations

(*444)
(8*2)
(*4222)
(4*4)
(*882)
(2*42) 		+
(842)

=
=
=
=
=
=
h{8,4} s{8,4} hr{8,4} s{4,8} h{4,8} hrr{8,4} sr{8,4}
Alternation duals
V(4.4)4 V3.(3.8)2 V(4.4.4)2 V(3.4)3 V88 V4.44 V3.3.4.3.8

References

  • John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
  • "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.

See also

Wikimedia Commons has media related to Uniform tiling 3-3-4-3-8.