Heptagonal tiling

In this article we will explore Heptagonal tiling, a topic that has generated great interest in different areas. Throughout history, Heptagonal tiling has been the subject of debate, research and analysis, due to its importance and relevance in today's society. From its origins to the present, Heptagonal tiling has played a fundamental role in different aspects of daily life, influencing culture, politics, economics and technology. Through this article, we will delve into the complexity of Heptagonal tiling, analyzing its different aspects and its impact on our modern world.

Heptagonal tiling
Heptagonal tiling
Poincaré disk model of the hyperbolic plane
Type Hyperbolic regular tiling
Vertex configuration 73
Schläfli symbol {7,3}
Wythoff symbol 3 | 7 2
Coxeter diagram
Symmetry group , (*732)
Dual Order-7 triangular tiling
Properties Vertex-transitive, edge-transitive, face-transitive

In geometry, a heptagonal tiling is a regular tiling of the hyperbolic plane. It is represented by Schläfli symbol of {7,3}, having three regular heptagons around each vertex.

Images


Poincaré half-plane model
Poincaré disk model
Beltrami-Klein model

This tiling is topologically related as a part of sequence of regular polyhedra with Schläfli symbol {n,3}.

*n32 symmetry mutation of regular tilings: {n,3}
Spherical Euclidean Compact hyperb. Paraco. Noncompact hyperbolic
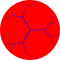
{2,3} {3,3} {4,3} {5,3} {6,3} {7,3} {8,3} {∞,3} {12i,3} {9i,3} {6i,3} {3i,3}

From a Wythoff construction there are eight hyperbolic uniform tilings that can be based from the regular heptagonal tiling.

Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 8 forms.

Uniform heptagonal/triangular tilings
Symmetry: , (*732) +, (732)
{7,3} t{7,3} r{7,3} t{3,7} {3,7} rr{7,3} tr{7,3} sr{7,3}
Uniform duals
V73 V3.14.14 V3.7.3.7 V6.6.7 V37 V3.4.7.4 V4.6.14 V3.3.3.3.7

Hurwitz surfaces

The symmetry group of the heptagonal tiling has fundamental domain the (2,3,7) Schwarz triangle, which yields this tiling.
Further information: Hurwitz surface

The symmetry group of the tiling is the (2,3,7) triangle group, and a fundamental domain for this action is the (2,3,7) Schwarz triangle. This is the smallest hyperbolic Schwarz triangle, and thus, by the proof of Hurwitz's automorphisms theorem, the tiling is the universal tiling that covers all Hurwitz surfaces (the Riemann surfaces with maximal symmetry group), giving them a tiling by heptagons whose symmetry group equals their automorphism group as Riemann surfaces. The smallest Hurwitz surface is the Klein quartic (genus 3, automorphism group of order 168), and the induced tiling has 24 heptagons, meeting at 56 vertices.

The dual order-7 triangular tiling has the same symmetry group, and thus yields triangulations of Hurwitz surfaces.

See also

Wikimedia Commons has media related to Order-3 heptagonal tiling.

References

  • John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
  • "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.