Rhombitetrahexagonal tiling

In this article, we will explore the fascinating world of Rhombitetrahexagonal tiling, a topic that has captured the attention of many people over time. From its impact on society to its implications in everyday life, Rhombitetrahexagonal tiling has been the subject of debate and analysis by experts in various disciplines. Whether we're talking about its influence on history, its relevance in today's world, or its projections into the future, Rhombitetrahexagonal tiling remains a topic of interest and curiosity for many. Throughout this article, we will examine different aspects of Rhombitetrahexagonal tiling, from its origins to its possible repercussions, with the aim of providing a broad and detailed overview of this exciting topic.

Rhombitetrahexagonal tiling
Rhombitetrahexagonal tiling
Poincaré disk model of the hyperbolic plane
Type Hyperbolic uniform tiling
Vertex configuration 4.4.6.4
Schläfli symbol rr{6,4} or
Wythoff symbol 4 | 6 2
Coxeter diagram

Symmetry group , (*642)
Dual Deltoidal tetrahexagonal tiling
Properties Vertex-transitive

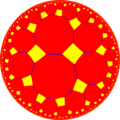
In geometry, the rhombitetrahexagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of rr{6,4}. It can be seen as constructed as a rectified tetrahexagonal tiling, r{6,4}, as well as an expanded order-4 hexagonal tiling or expanded order-6 square tiling.

Constructions

There are two uniform constructions of this tiling, one from or (*642) symmetry, and secondly removing the mirror middle, , gives a rectangular fundamental domain , (*3222).

Two uniform constructions of 4.4.4.6
Name Rhombitetrahexagonal tiling
Image
Symmetry
(*642)
 =
(*3222)
=
Schläfli symbol rr{6,4} t0,1,2,3{∞,3,∞}
Coxeter diagram =

There are 3 lower symmetry forms seen by including edge-colorings: sees the hexagons as truncated triangles, with two color edges, with (4*3) symmetry. sees the yellow squares as rectangles, with two color edges, with (6*2) symmetry. A final quarter symmetry combines these colorings, with (32×) symmetry, with 2 and 3 fold gyration points and glide reflections.

This four color tiling is related to a semiregular infinite skew polyhedron with the same vertex figure in Euclidean 3-space with a prismatic honeycomb construction of .

Symmetry

The dual tiling, called a deltoidal tetrahexagonal tiling, represents the fundamental domains of the *3222 orbifold, shown here from three different centers. Its fundamental domain is a Lambert quadrilateral, with 3 right angles. This symmetry can be seen from a , (*642) triangular symmetry with one mirror removed, constructed as , (*3222). Removing half of the blue mirrors doubles the domain again into *3322 symmetry.

*n42 symmetry mutation of expanded tilings: n.4.4.4
Symmetry
, (*n42) 		Spherical Euclidean Compact hyperbolic Paracomp.
*342
 *442
 *542
 *642
 *742
 *842
 *∞42
Expanded
figures
Config. 3.4.4.4 4.4.4.4 5.4.4.4 6.4.4.4 7.4.4.4 8.4.4.4 ∞.4.4.4
Rhombic
figures
config.
V3.4.4.4
V4.4.4.4
V5.4.4.4
V6.4.4.4
V7.4.4.4
V8.4.4.4
V∞.4.4.4
Uniform tetrahexagonal tilings
Symmetry: , (*642)
(with (*662), (*443) , (*3222) index 2 subsymmetries)
(And (*3232) index 4 subsymmetry)

=

=
=
=
=
=

=

=

=
=
=


=
{6,4} t{6,4} r{6,4} t{4,6} {4,6} rr{6,4} tr{6,4}
Uniform duals
V64 V4.12.12 V(4.6)2 V6.8.8 V46 V4.4.4.6 V4.8.12
Alternations

(*443)
(6*2)
(*3222)
(4*3)
(*662)
(2*32) 		+
(642)

=
=
=
=
=
=
h{6,4} s{6,4} hr{6,4} s{4,6} h{4,6} hrr{6,4} sr{6,4}
Uniform tilings in symmetry *3222
64
 6.6.4.4
 (3.4.4)2
 4.3.4.3.3.3
6.6.4.4
 6.4.4.4
 3.4.4.4.4
(3.4.4)2
 3.4.4.4.4
 46

See also

Wikimedia Commons has media related to Uniform tiling 4-4-4-6.

References

  • John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
  • "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.