Convex combination
Appearance move to sidebar hide Given three points
x
1
,
x
2
,
x
3
{\displaystyle x_{1},x_{2},x_{3}}
in a plane as shown in the figure, the point
P
{\displaystyle P}
is a convex combination of the three points, while
Q
{\displaystyle Q}
is not. (
Q
{\displaystyle Q}
is however an affine combination of the three points, as their affine hull is the entire plane.)
Given three points
x
1
,
x
2
,
x
3
{\displaystyle x_{1},x_{2},x_{3}}
in a plane as shown in the figure, the point
P
{\displaystyle P}
is a convex combination of the three points, while
Q
{\displaystyle Q}
is not. (
Q
{\displaystyle Q}
is however an affine combination of the three points, as their affine hull is the entire plane.)
 Convex combination of two points
v
1
,
v
2
∈
R
2
{\displaystyle v_{1},v_{2}\in \mathbb {R} ^{2}}
in a two dimensional vector space
R
2
{\displaystyle \mathbb {R} ^{2}}
as animation in Geogebra with
t
∈
{\displaystyle t\in }
and
K
(
t
)
:=
(
1
−
t
)
⋅
v
1
+
t
⋅
v
2
{\displaystyle K(t):=(1-t)\cdot v_{1}+t\cdot v_{2}}
Convex combination of two points
v
1
,
v
2
∈
R
2
{\displaystyle v_{1},v_{2}\in \mathbb {R} ^{2}}
in a two dimensional vector space
R
2
{\displaystyle \mathbb {R} ^{2}}
as animation in Geogebra with
t
∈
{\displaystyle t\in }
and
K
(
t
)
:=
(
1
−
t
)
⋅
v
1
+
t
⋅
v
2
{\displaystyle K(t):=(1-t)\cdot v_{1}+t\cdot v_{2}}
 Convex combination of three points
v
0
,
v
1
,
v
2
of
2
-simplex
∈
R
2
{\displaystyle v_{0},v_{1},v_{2}{\text{ of }}2{\text{-simplex}}\in \mathbb {R} ^{2}}
in a two dimensional vector space
R
2
{\displaystyle \mathbb {R} ^{2}}
as shown in animation with
α
0
+
α
1
+
α
2
=
1
{\displaystyle \alpha ^{0}+\alpha ^{1}+\alpha ^{2}=1}
,
P
(
α
0
,
α
1
,
α
2
)
{\displaystyle P(\alpha ^{0},\alpha ^{1},\alpha ^{2})}
:=
α
0
v
0
+
α
1
v
1
+
α
2
v
2
{\displaystyle :=\alpha ^{0}v_{0}+\alpha ^{1}v_{1}+\alpha ^{2}v_{2}}
. When P is inside of the triangle
α
i
≥
0
{\displaystyle \alpha _{i}\geq 0}
. Otherwise, when P is outside of the triangle, at least one of the
α
i
{\displaystyle \alpha _{i}}
is negative.
Convex combination of three points
v
0
,
v
1
,
v
2
of
2
-simplex
∈
R
2
{\displaystyle v_{0},v_{1},v_{2}{\text{ of }}2{\text{-simplex}}\in \mathbb {R} ^{2}}
in a two dimensional vector space
R
2
{\displaystyle \mathbb {R} ^{2}}
as shown in animation with
α
0
+
α
1
+
α
2
=
1
{\displaystyle \alpha ^{0}+\alpha ^{1}+\alpha ^{2}=1}
,
P
(
α
0
,
α
1
,
α
2
)
{\displaystyle P(\alpha ^{0},\alpha ^{1},\alpha ^{2})}
:=
α
0
v
0
+
α
1
v
1
+
α
2
v
2
{\displaystyle :=\alpha ^{0}v_{0}+\alpha ^{1}v_{1}+\alpha ^{2}v_{2}}
. When P is inside of the triangle
α
i
≥
0
{\displaystyle \alpha _{i}\geq 0}
. Otherwise, when P is outside of the triangle, at least one of the
α
i
{\displaystyle \alpha _{i}}
is negative.
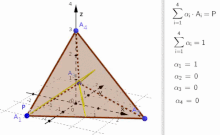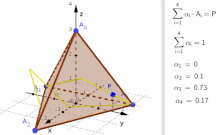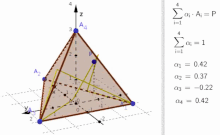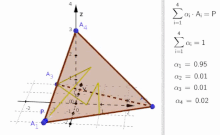 Convex combination of four points
A
1
,
A
2
,
A
3
,
A
4
∈
R
3
{\displaystyle A_{1},A_{2},A_{3},A_{4}\in \mathbb {R} ^{3}}
in a three dimensional vector space
R
3
{\displaystyle \mathbb {R} ^{3}}
as animation in Geogebra with
∑
i
=
1
4
α
i
=
1
{\displaystyle \sum _{i=1}^{4}\alpha _{i}=1}
and
∑
i
=
1
4
α
i
⋅
A
i
=
P
{\displaystyle \sum _{i=1}^{4}\alpha _{i}\cdot A_{i}=P}
. When P is inside of the tetrahedron
α
i
>=
0
{\displaystyle \alpha _{i}>=0}
. Otherwise, when P is outside of the tetrahedron, at least one of the
α
i
{\displaystyle \alpha _{i}}
is negative.
Convex combination of four points
A
1
,
A
2
,
A
3
,
A
4
∈
R
3
{\displaystyle A_{1},A_{2},A_{3},A_{4}\in \mathbb {R} ^{3}}
in a three dimensional vector space
R
3
{\displaystyle \mathbb {R} ^{3}}
as animation in Geogebra with
∑
i
=
1
4
α
i
=
1
{\displaystyle \sum _{i=1}^{4}\alpha _{i}=1}
and
∑
i
=
1
4
α
i
⋅
A
i
=
P
{\displaystyle \sum _{i=1}^{4}\alpha _{i}\cdot A_{i}=P}
. When P is inside of the tetrahedron
α
i
>=
0
{\displaystyle \alpha _{i}>=0}
. Otherwise, when P is outside of the tetrahedron, at least one of the
α
i
{\displaystyle \alpha _{i}}
is negative.
 Convex combination of two functions as vectors in a vector space of functions - visualized in Open Source Geogebra with
=
{\displaystyle =}
and as the first function
f
:
→
R
{\displaystyle f:\to \mathbb {R} }
a polynomial is defined.
f
(
x
)
:=
3
10
⋅
x
2
−
2
{\displaystyle f(x):={\frac {3}{10}}\cdot x^{2}-2}
A trigonometric function
g
:
→
R
{\displaystyle g:\to \mathbb {R} }
was chosen as the second function.
g
(
x
)
:=
2
⋅
cos
(
x
)
+
1
{\displaystyle g(x):=2\cdot \cos(x)+1}
The figure illustrates the convex combination
K
(
t
)
:=
(
1
−
t
)
⋅
f
+
t
⋅
g
{\displaystyle K(t):=(1-t)\cdot f+t\cdot g}
of
f
{\displaystyle f}
and
g
{\displaystyle g}
as graph in red color.
Convex combination of two functions as vectors in a vector space of functions - visualized in Open Source Geogebra with
=
{\displaystyle =}
and as the first function
f
:
→
R
{\displaystyle f:\to \mathbb {R} }
a polynomial is defined.
f
(
x
)
:=
3
10
⋅
x
2
−
2
{\displaystyle f(x):={\frac {3}{10}}\cdot x^{2}-2}
A trigonometric function
g
:
→
R
{\displaystyle g:\to \mathbb {R} }
was chosen as the second function.
g
(
x
)
:=
2
⋅
cos
(
x
)
+
1
{\displaystyle g(x):=2\cdot \cos(x)+1}
The figure illustrates the convex combination
K
(
t
)
:=
(
1
−
t
)
⋅
f
+
t
⋅
g
{\displaystyle K(t):=(1-t)\cdot f+t\cdot g}
of
f
{\displaystyle f}
and
g
{\displaystyle g}
as graph in red color.
In convex geometry and vector algebra, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the count of the weights as in a standard weighted average.
Formal definition
More formally, given a finite number of points x 1 , x 2 , … , x n {\displaystyle x_{1},x_{2},\dots ,x_{n}} in a real vector space, a convex combination of these points is a point of the form
α 1 x 1 + α 2 x 2 + ⋯ + α n x n {\displaystyle \alpha _{1}x_{1}+\alpha _{2}x_{2}+\cdots +\alpha _{n}x_{n}}where the real numbers α i {\displaystyle \alpha _{i}} satisfy α i ≥ 0 {\displaystyle \alpha _{i}\geq 0} and α 1 + α 2 + ⋯ + α n = 1. {\displaystyle \alpha _{1}+\alpha _{2}+\cdots +\alpha _{n}=1.}
As a particular example, every convex combination of two points lies on the line segment between the points.
A set is convex if it contains all convex combinations of its points. The convex hull of a given set of points is identical to the set of all their convex combinations.
There exist subsets of a vector space that are not closed under linear combinations but are closed under convex combinations. For example, the interval {\displaystyle } is convex but generates the real-number line under linear combinations. Another example is the convex set of probability distributions, as linear combinations preserve neither nonnegativity nor affinity (i.e., having total integral one).
Other objects
- A random variable X {\displaystyle X} is said to have an n {\displaystyle n} -component finite mixture distribution if its probability density function is a convex combination of n {\displaystyle n} so-called component densities.
Related constructions
- A conical combination is a linear combination with nonnegative coefficients. When a point x {\displaystyle x} is to be used as the reference origin for defining displacement vectors, then x {\displaystyle x} is a convex combination of n {\displaystyle n} points x 1 , x 2 , … , x n {\displaystyle x_{1},x_{2},\dots ,x_{n}} if and only if the zero displacement is a non-trivial conical combination of their n {\displaystyle n} respective displacement vectors relative to x {\displaystyle x} .
- Weighted means are functionally the same as convex combinations, but they use a different notation. The coefficients (weights) in a weighted mean are not required to sum to 1; instead the weighted linear combination is explicitly divided by the sum of the weights.
- Affine combinations are like convex combinations, but the coefficients are not required to be non-negative. Hence affine combinations are defined in vector spaces over any field.
See also
References
- ^ a b c d Rockafellar, R. Tyrrell (1970), Convex Analysis, Princeton Mathematical Series, vol. 28, Princeton University Press, Princeton, N.J., pp. 11–12, MR 0274683
External links
- Convex sum/combination with a trianglr - interactive illustration
- Convex sum/combination with a hexagon - interactive illustration
- Convex sum/combination with a tetraeder - interactive illustration
| Convex analysis and variational analysis | |
|---|---|
| Basic concepts | |
| Topics (list) | |
| Maps | |
| Main results (list) | |
| Sets | |
| Series | |
| Duality | |
| Applications and related | |
 in a plane as shown in the figure, the point
P
{\displaystyle P}
in a plane as shown in the figure, the point
P
{\displaystyle P}
 is a convex combination of the three points, while
Q
{\displaystyle Q}
is a convex combination of the three points, while
Q
{\displaystyle Q}
 is not. (
Q
{\displaystyle Q}
is not. (
Q
{\displaystyle Q}
 in a two dimensional vector space
R
2
{\displaystyle \mathbb {R} ^{2}}
in a two dimensional vector space
R
2
{\displaystyle \mathbb {R} ^{2}}
 as animation in
as animation in  and
K
(
t
)
:=
(
1
−
t
)
⋅
v
1
+
t
⋅
v
2
{\displaystyle K(t):=(1-t)\cdot v_{1}+t\cdot v_{2}}
and
K
(
t
)
:=
(
1
−
t
)
⋅
v
1
+
t
⋅
v
2
{\displaystyle K(t):=(1-t)\cdot v_{1}+t\cdot v_{2}}

 in a two dimensional vector space
R
2
{\displaystyle \mathbb {R} ^{2}}
in a two dimensional vector space
R
2
{\displaystyle \mathbb {R} ^{2}}
 ,
P
(
α
0
,
α
1
,
α
2
)
{\displaystyle P(\alpha ^{0},\alpha ^{1},\alpha ^{2})}
,
P
(
α
0
,
α
1
,
α
2
)
{\displaystyle P(\alpha ^{0},\alpha ^{1},\alpha ^{2})}
 :=
α
0
v
0
+
α
1
v
1
+
α
2
v
2
{\displaystyle :=\alpha ^{0}v_{0}+\alpha ^{1}v_{1}+\alpha ^{2}v_{2}}
:=
α
0
v
0
+
α
1
v
1
+
α
2
v
2
{\displaystyle :=\alpha ^{0}v_{0}+\alpha ^{1}v_{1}+\alpha ^{2}v_{2}}
 . When P is inside of the triangle
α
i
≥
0
{\displaystyle \alpha _{i}\geq 0}
. When P is inside of the triangle
α
i
≥
0
{\displaystyle \alpha _{i}\geq 0}
 . Otherwise, when P is outside of the triangle, at least one of the
α
i
{\displaystyle \alpha _{i}}
. Otherwise, when P is outside of the triangle, at least one of the
α
i
{\displaystyle \alpha _{i}}
 is negative.
is negative.
 in a three dimensional vector space
R
3
{\displaystyle \mathbb {R} ^{3}}
in a three dimensional vector space
R
3
{\displaystyle \mathbb {R} ^{3}}
 as animation in
as animation in  and
∑
i
=
1
4
α
i
⋅
A
i
=
P
{\displaystyle \sum _{i=1}^{4}\alpha _{i}\cdot A_{i}=P}
and
∑
i
=
1
4
α
i
⋅
A
i
=
P
{\displaystyle \sum _{i=1}^{4}\alpha _{i}\cdot A_{i}=P}
 . When P is inside of the tetrahedron
α
i
>=
0
{\displaystyle \alpha _{i}>=0}
. When P is inside of the tetrahedron
α
i
>=
0
{\displaystyle \alpha _{i}>=0}
 . Otherwise, when P is outside of the tetrahedron, at least one of the
α
i
{\displaystyle \alpha _{i}}
. Otherwise, when P is outside of the tetrahedron, at least one of the
α
i
{\displaystyle \alpha _{i}}
 and as the first function
f
:
→
R
{\displaystyle f:\to \mathbb {R} }
and as the first function
f
:
→
R
{\displaystyle f:\to \mathbb {R} }
 a polynomial is defined.
f
(
x
)
:=
3
10
⋅
x
2
−
2
{\displaystyle f(x):={\frac {3}{10}}\cdot x^{2}-2}
a polynomial is defined.
f
(
x
)
:=
3
10
⋅
x
2
−
2
{\displaystyle f(x):={\frac {3}{10}}\cdot x^{2}-2}
 A trigonometric function
g
:
→
R
{\displaystyle g:\to \mathbb {R} }
A trigonometric function
g
:
→
R
{\displaystyle g:\to \mathbb {R} }
 was chosen as the second function.
g
(
x
)
:=
2
⋅
cos
(
x
)
+
1
{\displaystyle g(x):=2\cdot \cos(x)+1}
was chosen as the second function.
g
(
x
)
:=
2
⋅
cos
(
x
)
+
1
{\displaystyle g(x):=2\cdot \cos(x)+1}
 The figure illustrates the convex combination
K
(
t
)
:=
(
1
−
t
)
⋅
f
+
t
⋅
g
{\displaystyle K(t):=(1-t)\cdot f+t\cdot g}
The figure illustrates the convex combination
K
(
t
)
:=
(
1
−
t
)
⋅
f
+
t
⋅
g
{\displaystyle K(t):=(1-t)\cdot f+t\cdot g}
 of
f
{\displaystyle f}
of
f
{\displaystyle f}
 and
g
{\displaystyle g}
and
g
{\displaystyle g}
 as graph in red color.
as graph in red color.
 in a
in a 

 is convex but generates the real-number line under linear combinations. Another example is the convex set of
is convex but generates the real-number line under linear combinations. Another example is the convex set of  is said to have an
n
{\displaystyle n}
is said to have an
n
{\displaystyle n}
 -component
-component  is to be used as the reference origin for defining
is to be used as the reference origin for defining