Univariate distribution
In this article, we invite you to enter the exciting world of Univariate distribution. Along these lines, we will explore various aspects related to Univariate distribution, from its origin to its influence on current society. We will delve into its implications, its relevance today and its potential impact in the future. Likewise, we will analyze different perspectives and opinions from experts in the field, with the aim of providing you with a broad and enriching vision about Univariate distribution. Get ready to discover everything you need to know about Univariate distribution in this article!
In statistics, a univariate distribution is a probability distribution of only one random variable. This is in contrast to a multivariate distribution, the probability distribution of a random vector (consisting of multiple random variables).
Examples
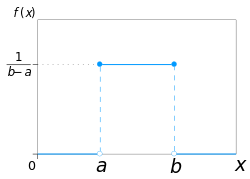
One of the simplest examples of a discrete univariate distribution is the discrete uniform distribution, where all elements of a finite set are equally likely. It is the probability model for the outcomes of tossing a fair coin, rolling a fair die, etc. The univariate continuous uniform distribution on an interval has the property that all sub-intervals of the same length are equally likely.
Other examples of discrete univariate distributions include the binomial, geometric, negative binomial, and Poisson distributions.[1] At least 750 univariate discrete distributions have been reported in the literature.[2]
Examples of commonly applied continuous univariate distributions[3] include the normal distribution, Student's t distribution, chisquare distribution, F distribution, exponential and gamma distributions.
See also
References
- ^ Johnson, N.L., Kemp, A.W., and Kotz, S. (2005) Discrete Univariate Distributions, 3rd Edition, Wiley, ISBN 978-0-471-27246-5.
- ^ Wimmer G, Altmann G (1999) Thesaurus of univariate discrete probability distributions. STAMM Verlag GmbH Essen, 1st ed XXVII ISBN 3-87773-025-6
- ^ Johnson N.L., Kotz S, Balakrishnan N. (1994) Continuous Univariate Distributions Vol 1. Wiley Series in Probability and Statistics.
Further reading
- Leemis, L. M.; McQueston, J. T. (2008). "Univariate Distribution Relationships" (PDF). The American Statistician. 62: 45–53. doi:10.1198/000313008X270448.
 | This statistics-related article is a stub. You can help Wikipedia by expanding it. |