Trigonometric substitution

Trigonometry

Outline History Usage Functions (sin, cos, tan, inverse) Generalized trigonometry
Reference
Identities Exact constants Tables Unit circle
Laws and theorems
Sines Cosines Tangents Cotangents Pythagorean theorem
Calculus
Trigonometric substitution Integrals (inverse functions) Derivatives Trigonometric series
Mathematicians
Hipparchus Ptolemy Brahmagupta al-Hasib al-Battani Regiomontanus Viète de Moivre Euler Fourier
v t e

Differential

Definitions
Derivative (generalizations) Differential infinitesimal of a function total
Concepts
Differentiation notation Second derivative Implicit differentiation Logarithmic differentiation Related rates Taylor's theorem
Rules and identities
Sum Product Chain Power Quotient L'Hôpital's rule Inverse General Leibniz Faà di Bruno's formula Reynolds

Integral

Definitions
Lists of integrals Integral transform Leibniz integral rule
Antiderivative Integral (improper) Riemann integral Lebesgue integration Contour integration Integral of inverse functions
Integration by
Parts Discs Cylindrical shells Substitution (trigonometric, tangent half-angle, Euler) Euler's formula Partial fractions Changing order Reduction formulae Differentiating under the integral sign Risch algorithm

Series

Convergence tests
Geometric (arithmetico-geometric) Harmonic Alternating Power Binomial Taylor
Summand limit (term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel

Vector

Multivariable

Advanced

Specialized

Miscellaneous

In mathematics, a trigonometric substitution replaces a trigonometric function for another expression. In calculus, trigonometric substitutions are a technique for evaluating integrals. In this case, an expression involving a radical function is replaced with a trigonometric one. Trigonometric identities may help simplify the answer. Like other methods of integration by substitution, when evaluating a definite integral, it may be simpler to completely deduce the antiderivative before applying the boundaries of integration.

Case I: Integrands containing a2 − x2

Let x = a sin ⁡ θ , {\displaystyle x=a\sin \theta ,} $x=a\sin \theta ,$ and use the identity 1 − sin 2 ⁡ θ = cos 2 ⁡ θ . {\displaystyle 1-\sin ^{2}\theta =\cos ^{2}\theta .} $1-\sin ^{2}\theta =\cos ^{2}\theta .$

Examples of Case I

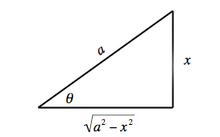Geometric construction for Case I Example 1

In the integral

∫ d x a 2 − x 2 , {\displaystyle \int {\frac {dx}{\sqrt {a^{2}-x^{2}}}},} $\int {\frac {dx}{\sqrt {a^{2}-x^{2}}}},$

we may use

x = a sin ⁡ θ , d x = a cos ⁡ θ d θ , θ = arcsin ⁡ x a . {\displaystyle x=a\sin \theta ,\quad dx=a\cos \theta \,d\theta ,\quad \theta =\arcsin {\frac {x}{a}}.} $x=a\sin \theta ,\quad dx=a\cos \theta \,d\theta ,\quad \theta =\arcsin {\frac {x}{a}}.$

Then,

∫ d x a 2 − x 2 = ∫ a cos ⁡ θ d θ a 2 − a 2 sin 2 ⁡ θ = ∫ a cos ⁡ θ d θ a 2 ( 1 − sin 2 ⁡ θ ) = ∫ a cos ⁡ θ d θ a 2 cos 2 ⁡ θ = ∫ d θ = θ + C = arcsin ⁡ x a + C . {\displaystyle {\begin{aligned}\int {\frac {dx}{\sqrt {a^{2}-x^{2}}}}&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}-a^{2}\sin ^{2}\theta }}}\\&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}(1-\sin ^{2}\theta )}}}\\&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}\cos ^{2}\theta }}}\\&=\int d\theta \\&=\theta +C\\&=\arcsin {\frac {x}{a}}+C.\end{aligned}}}

{\begin{aligned}\int {\frac {dx}{\sqrt {a^{2}-x^{2}}}}&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}-a^{2}\sin ^{2}\theta }}}\\&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}(1-\sin ^{2}\theta )}}}\\&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}\cos ^{2}\theta }}}\\&=\int d\theta \\&=\theta +C\\&=\arcsin {\frac {x}{a}}+C.\end{aligned}}

The above step requires that a > 0 {\displaystyle a>0} $a>0$ and cos ⁡ θ > 0. {\displaystyle \cos \theta >0.} $\cos \theta >0.$ We can choose a {\displaystyle a} $a$ to be the principal root of a 2 , {\displaystyle a^{2},} $a^{2},$ and impose the restriction − π / 2 < θ < π / 2 {\displaystyle -\pi /2<\theta <\pi /2} $-\pi /2<\theta <\pi /2$ by using the inverse sine function.

For a definite integral, one must figure out how the bounds of integration change. For example, as x {\displaystyle x} $x$ goes from 0 {\displaystyle 0} $0$ to a / 2 , {\displaystyle a/2,} $a/2,$ then sin ⁡ θ {\displaystyle \sin \theta } $\sin \theta$ goes from 0 {\displaystyle 0} $0$ to 1 / 2 , {\displaystyle 1/2,} $1/2,$ so θ {\displaystyle \theta } $\theta$ goes from 0 {\displaystyle 0} $0$ to π / 6. {\displaystyle \pi /6.} $\pi /6.$ Then,

∫ 0 a / 2 d x a 2 − x 2 = ∫ 0 π / 6 d θ = π 6 . {\displaystyle \int _{0}^{a/2}{\frac {dx}{\sqrt {a^{2}-x^{2}}}}=\int _{0}^{\pi /6}d\theta ={\frac {\pi }{6}}.} $\int _{0}^{a/2}{\frac {dx}{\sqrt {a^{2}-x^{2}}}}=\int _{0}^{\pi /6}d\theta ={\frac {\pi }{6}}.$

Some care is needed when picking the bounds. Because integration above requires that − π / 2 < θ < π / 2 {\displaystyle -\pi /2<\theta <\pi /2} $-\pi /2<\theta <\pi /2$ , θ {\displaystyle \theta } $\theta$ can only go from 0 {\displaystyle 0} $0$ to π / 6. {\displaystyle \pi /6.} $\pi /6.$ Neglecting this restriction, one might have picked θ {\displaystyle \theta } $\theta$ to go from π {\displaystyle \pi } $\pi$ to 5 π / 6 , {\displaystyle 5\pi /6,} $5\pi /6,$ which would have resulted in the negative of the actual value.

Alternatively, fully evaluate the indefinite integrals before applying the boundary conditions. In that case, the antiderivative gives

∫ 0 a / 2 d x a 2 − x 2 = arcsin ⁡ ( x a ) | 0 a / 2 = arcsin ⁡ ( 1 2 ) − arcsin ⁡ ( 0 ) = π 6 {\displaystyle \int _{0}^{a/2}{\frac {dx}{\sqrt {a^{2}-x^{2}}}}=\arcsin \left({\frac {x}{a}}\right){\Biggl |}_{0}^{a/2}=\arcsin \left({\frac {1}{2}}\right)-\arcsin(0)={\frac {\pi }{6}}} $\int _{0}^{a/2}{\frac {dx}{\sqrt {a^{2}-x^{2}}}}=\arcsin \left({\frac {x}{a}}\right){\Biggl |}_{0}^{a/2}=\arcsin \left({\frac {1}{2}}\right)-\arcsin(0)={\frac {\pi }{6}}$ as before. Example 2

The integral

∫ a 2 − x 2 d x , {\displaystyle \int {\sqrt {a^{2}-x^{2}}}\,dx,} $\int {\sqrt {a^{2}-x^{2}}}\,dx,$

may be evaluated by letting x = a sin ⁡ θ , d x = a cos ⁡ θ d θ , θ = arcsin ⁡ x a , {\textstyle x=a\sin \theta ,\,dx=a\cos \theta \,d\theta ,\,\theta =\arcsin {\frac {x}{a}},} ${\textstyle x=a\sin \theta ,\,dx=a\cos \theta \,d\theta ,\,\theta =\arcsin {\frac {x}{a}},}$ where a > 0 {\displaystyle a>0} $a>0$ so that a 2 = a , {\textstyle {\sqrt {a^{2}}}=a,} ${\textstyle {\sqrt {a^{2}}}=a,}$ and − π 2 ≤ θ ≤ π 2 {\textstyle -{\frac {\pi }{2}}\leq \theta \leq {\frac {\pi }{2}}} ${\textstyle -{\frac {\pi }{2}}\leq \theta \leq {\frac {\pi }{2}}}$ by the range of arcsine, so that cos ⁡ θ ≥ 0 {\displaystyle \cos \theta \geq 0} $\cos \theta \geq 0$ and cos 2 ⁡ θ = cos ⁡ θ . {\textstyle {\sqrt {\cos ^{2}\theta }}=\cos \theta .} ${\textstyle {\sqrt {\cos ^{2}\theta }}=\cos \theta .}$

Then,

∫ a 2 − x 2 d x = ∫ a 2 − a 2 sin 2 ⁡ θ ( a cos ⁡ θ ) d θ = ∫ a 2 ( 1 − sin 2 ⁡ θ ) ( a cos ⁡ θ ) d θ = ∫ a 2 ( cos 2 ⁡ θ ) ( a cos ⁡ θ ) d θ = ∫ ( a cos ⁡ θ ) ( a cos ⁡ θ ) d θ = a 2 ∫ cos 2 ⁡ θ d θ = a 2 ∫ ( 1 + cos ⁡ 2 θ 2 ) d θ = a 2 2 ( θ + 1 2 sin ⁡ 2 θ ) + C = a 2 2 ( θ + sin ⁡ θ cos ⁡ θ ) + C = a 2 2 ( arcsin ⁡ x a + x a 1 − x 2 a 2 ) + C = a 2 2 arcsin ⁡ x a + x 2 a 2 − x 2 + C . {\displaystyle {\begin{aligned}\int {\sqrt {a^{2}-x^{2}}}\,dx&=\int {\sqrt {a^{2}-a^{2}\sin ^{2}\theta }}\,(a\cos \theta )\,d\theta \\&=\int {\sqrt {a^{2}(1-\sin ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\&=\int {\sqrt {a^{2}(\cos ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\&=\int (a\cos \theta )(a\cos \theta )\,d\theta \\&=a^{2}\int \cos ^{2}\theta \,d\theta \\&=a^{2}\int \left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\&={\frac {a^{2}}{2}}\left(\theta +{\frac {1}{2}}\sin 2\theta \right)+C\\&={\frac {a^{2}}{2}}(\theta +\sin \theta \cos \theta )+C\\&={\frac {a^{2}}{2}}\left(\arcsin {\frac {x}{a}}+{\frac {x}{a}}{\sqrt {1-{\frac {x^{2}}{a^{2}}}}}\right)+C\\&={\frac {a^{2}}{2}}\arcsin {\frac {x}{a}}+{\frac {x}{2}}{\sqrt {a^{2}-x^{2}}}+C.\end{aligned}}}

{\begin{aligned}\int {\sqrt {a^{2}-x^{2}}}\,dx&=\int {\sqrt {a^{2}-a^{2}\sin ^{2}\theta }}\,(a\cos \theta )\,d\theta \\&=\int {\sqrt {a^{2}(1-\sin ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\&=\int {\sqrt {a^{2}(\cos ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\&=\int (a\cos \theta )(a\cos \theta )\,d\theta \\&=a^{2}\int \cos ^{2}\theta \,d\theta \\&=a^{2}\int \left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\&={\frac {a^{2}}{2}}\left(\theta +{\frac {1}{2}}\sin 2\theta \right)+C\\&={\frac {a^{2}}{2}}(\theta +\sin \theta \cos \theta )+C\\&={\frac {a^{2}}{2}}\left(\arcsin {\frac {x}{a}}+{\frac {x}{a}}{\sqrt {1-{\frac {x^{2}}{a^{2}}}}}\right)+C\\&={\frac {a^{2}}{2}}\arcsin {\frac {x}{a}}+{\frac {x}{2}}{\sqrt {a^{2}-x^{2}}}+C.\end{aligned}}

For a definite integral, the bounds change once the substitution is performed and are determined using the equation θ = arcsin ⁡ x a , {\textstyle \theta =\arcsin {\frac {x}{a}},} ${\textstyle \theta =\arcsin {\frac {x}{a}},}$ with values in the range − π 2 ≤ θ ≤ π 2 . {\textstyle -{\frac {\pi }{2}}\leq \theta \leq {\frac {\pi }{2}}.} ${\textstyle -{\frac {\pi }{2}}\leq \theta \leq {\frac {\pi }{2}}.}$ Alternatively, apply the boundary terms directly to the formula for the antiderivative.

For example, the definite integral

∫ − 1 1 4 − x 2 d x , {\displaystyle \int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx,} $\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx,$

may be evaluated by substituting x = 2 sin ⁡ θ , d x = 2 cos ⁡ θ d θ , {\displaystyle x=2\sin \theta ,\,dx=2\cos \theta \,d\theta ,} $x=2\sin \theta ,\,dx=2\cos \theta \,d\theta ,$ with the bounds determined using θ = arcsin ⁡ x 2 . {\textstyle \theta =\arcsin {\frac {x}{2}}.} ${\textstyle \theta =\arcsin {\frac {x}{2}}.}$

Because arcsin ⁡ ( 1 / 2 ) = π / 6 {\displaystyle \arcsin(1/{2})=\pi /6} $\arcsin(1/{2})=\pi /6$ and arcsin ⁡ ( − 1 / 2 ) = − π / 6 , {\displaystyle \arcsin(-1/2)=-\pi /6,} $\arcsin(-1/2)=-\pi /6,$

∫ − 1 1 4 − x 2 d x = ∫ − π / 6 π / 6 4 − 4 sin 2 ⁡ θ ( 2 cos ⁡ θ ) d θ = ∫ − π / 6 π / 6 4 ( 1 − sin 2 ⁡ θ ) ( 2 cos ⁡ θ ) d θ = ∫ − π / 6 π / 6 4 ( cos 2 ⁡ θ ) ( 2 cos ⁡ θ ) d θ = ∫ − π / 6 π / 6 ( 2 cos ⁡ θ ) ( 2 cos ⁡ θ ) d θ = 4 ∫ − π / 6 π / 6 cos 2 ⁡ θ d θ = 4 ∫ − π / 6 π / 6 ( 1 + cos ⁡ 2 θ 2 ) d θ = 2 − π / 6 π / 6 = | − π / 6 π / 6 = ( π 3 + sin ⁡ π 3 ) − ( − π 3 + sin ⁡ ( − π 3 ) ) = 2 π 3 + 3 . {\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\int _{-\pi /6}^{\pi /6}{\sqrt {4-4\sin ^{2}\theta }}\,(2\cos \theta )\,d\theta \\&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(1-\sin ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(\cos ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\&=\int _{-\pi /6}^{\pi /6}(2\cos \theta )(2\cos \theta )\,d\theta \\&=4\int _{-\pi /6}^{\pi /6}\cos ^{2}\theta \,d\theta \\&=4\int _{-\pi /6}^{\pi /6}\left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\&=2\left_{-\pi /6}^{\pi /6}={\Biggl |}_{-\pi /6}^{\pi /6}\\&=\left({\frac {\pi }{3}}+\sin {\frac {\pi }{3}}\right)-\left(-{\frac {\pi }{3}}+\sin \left(-{\frac {\pi }{3}}\right)\right)={\frac {2\pi }{3}}+{\sqrt {3}}.\end{aligned}}}

{\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\int _{-\pi /6}^{\pi /6}{\sqrt {4-4\sin ^{2}\theta }}\,(2\cos \theta )\,d\theta \\&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(1-\sin ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(\cos ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\&=\int _{-\pi /6}^{\pi /6}(2\cos \theta )(2\cos \theta )\,d\theta \\&=4\int _{-\pi /6}^{\pi /6}\cos ^{2}\theta \,d\theta \\&=4\int _{-\pi /6}^{\pi /6}\left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\&=2\left_{-\pi /6}^{\pi /6}={\Biggl |}_{-\pi /6}^{\pi /6}\\&=\left({\frac {\pi }{3}}+\sin {\frac {\pi }{3}}\right)-\left(-{\frac {\pi }{3}}+\sin \left(-{\frac {\pi }{3}}\right)\right)={\frac {2\pi }{3}}+{\sqrt {3}}.\end{aligned}}

On the other hand, direct application of the boundary terms to the previously obtained formula for the antiderivative yields

∫ − 1 1 4 − x 2 d x = − 1 1 = ( 2 arcsin ⁡ 1 2 + 1 2 4 − 1 ) − ( 2 arcsin ⁡ ( − 1 2 ) + − 1 2 4 − 1 ) = ( 2 ⋅ π 6 + 3 2 ) − ( 2 ⋅ ( − π 6 ) − 3 2 ) = 2 π 3 + 3 {\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\left_{-1}^{1}\\&=\left(2\arcsin {\frac {1}{2}}+{\frac {1}{2}}{\sqrt {4-1}}\right)-\left(2\arcsin \left(-{\frac {1}{2}}\right)+{\frac {-1}{2}}{\sqrt {4-1}}\right)\\&=\left(2\cdot {\frac {\pi }{6}}+{\frac {\sqrt {3}}{2}}\right)-\left(2\cdot \left(-{\frac {\pi }{6}}\right)-{\frac {\sqrt {3}}{2}}\right)\\&={\frac {2\pi }{3}}+{\sqrt {3}}\end{aligned}}}

{\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\left_{-1}^{1}\\&=\left(2\arcsin {\frac {1}{2}}+{\frac {1}{2}}{\sqrt {4-1}}\right)-\left(2\arcsin \left(-{\frac {1}{2}}\right)+{\frac {-1}{2}}{\sqrt {4-1}}\right)\\&=\left(2\cdot {\frac {\pi }{6}}+{\frac {\sqrt {3}}{2}}\right)-\left(2\cdot \left(-{\frac {\pi }{6}}\right)-{\frac {\sqrt {3}}{2}}\right)\\&={\frac {2\pi }{3}}+{\sqrt {3}}\end{aligned}}

as before.

Case II: Integrands containing a2 + x2

Let x = a tan ⁡ θ , {\displaystyle x=a\tan \theta ,} $x=a\tan \theta ,$ and use the identity 1 + tan 2 ⁡ θ = sec 2 ⁡ θ . {\displaystyle 1+\tan ^{2}\theta =\sec ^{2}\theta .} $1+\tan ^{2}\theta =\sec ^{2}\theta .$

Examples of Case II

Geometric construction for Case II Example 1

In the integral

∫ d x a 2 + x 2 {\displaystyle \int {\frac {dx}{a^{2}+x^{2}}}} $\int {\frac {dx}{a^{2}+x^{2}}}$

we may write

x = a tan ⁡ θ , d x = a sec 2 ⁡ θ d θ , θ = arctan ⁡ x a , {\displaystyle x=a\tan \theta ,\quad dx=a\sec ^{2}\theta \,d\theta ,\quad \theta =\arctan {\frac {x}{a}},} $x=a\tan \theta ,\quad dx=a\sec ^{2}\theta \,d\theta ,\quad \theta =\arctan {\frac {x}{a}},$

so that the integral becomes

∫ d x a 2 + x 2 = ∫ a sec 2 ⁡ θ d θ a 2 + a 2 tan 2 ⁡ θ = ∫ a sec 2 ⁡ θ d θ a 2 ( 1 + tan 2 ⁡ θ ) = ∫ a sec 2 ⁡ θ d θ a 2 sec 2 ⁡ θ = ∫ d θ a = θ a + C = 1 a arctan ⁡ x a + C , {\displaystyle {\begin{aligned}\int {\frac {dx}{a^{2}+x^{2}}}&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}+a^{2}\tan ^{2}\theta }}\\&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}(1+\tan ^{2}\theta )}}\\&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}\sec ^{2}\theta }}\\&=\int {\frac {d\theta }{a}}\\&={\frac {\theta }{a}}+C\\&={\frac {1}{a}}\arctan {\frac {x}{a}}+C,\end{aligned}}} ${\begin{aligned}\int {\frac {dx}{a^{2}+x^{2}}}&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}+a^{2}\tan ^{2}\theta }}\\&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}(1+\tan ^{2}\theta )}}\\&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}\sec ^{2}\theta }}\\&=\int {\frac {d\theta }{a}}\\&={\frac {\theta }{a}}+C\\&={\frac {1}{a}}\arctan {\frac {x}{a}}+C,\end{aligned}}$

provided a ≠ 0. {\displaystyle a\neq 0.} $a\neq 0.$

For a definite integral, the bounds change once the substitution is performed and are determined using the equation θ = arctan ⁡ x a , {\displaystyle \theta =\arctan {\frac {x}{a}},} $\theta =\arctan {\frac {x}{a}},$ with values in the range − π 2 < θ < π 2 . {\displaystyle -{\frac {\pi }{2}}<\theta <{\frac {\pi }{2}}.} $-{\frac {\pi }{2}}<\theta <{\frac {\pi }{2}}.$ Alternatively, apply the boundary terms directly to the formula for the antiderivative.

For example, the definite integral

∫ 0 1 4 d x 1 + x 2 {\displaystyle \int _{0}^{1}{\frac {4\,dx}{1+x^{2}}}\,} $\int _{0}^{1}{\frac {4\,dx}{1+x^{2}}}\,$

may be evaluated by substituting x = tan ⁡ θ , d x = sec 2 ⁡ θ d θ , {\displaystyle x=\tan \theta ,\,dx=\sec ^{2}\theta \,d\theta ,} $x=\tan \theta ,\,dx=\sec ^{2}\theta \,d\theta ,$ with the bounds determined using θ = arctan ⁡ x . {\displaystyle \theta =\arctan x.} $\theta =\arctan x.$

Since arctan ⁡ 0 = 0 {\displaystyle \arctan 0=0} $\arctan 0=0$ and arctan ⁡ 1 = π / 4 , {\displaystyle \arctan 1=\pi /4,} $\arctan 1=\pi /4,$

∫ 0 1 4 d x 1 + x 2 = 4 ∫ 0 1 d x 1 + x 2 = 4 ∫ 0 π / 4 sec 2 ⁡ θ d θ 1 + tan 2 ⁡ θ = 4 ∫ 0 π / 4 sec 2 ⁡ θ d θ sec 2 ⁡ θ = 4 ∫ 0 π / 4 d θ = ( 4 θ ) | 0 π / 4 = 4 ( π 4 − 0 ) = π . {\displaystyle {\begin{aligned}\int _{0}^{1}{\frac {4\,dx}{1+x^{2}}}&=4\int _{0}^{1}{\frac {dx}{1+x^{2}}}\\&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta \,d\theta }{1+\tan ^{2}\theta }}\\&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta \,d\theta }{\sec ^{2}\theta }}\\&=4\int _{0}^{\pi /4}d\theta \\&=(4\theta ){\Bigg |}_{0}^{\pi /4}=4\left({\frac {\pi }{4}}-0\right)=\pi .\end{aligned}}}

{\begin{aligned}\int _{0}^{1}{\frac {4\,dx}{1+x^{2}}}&=4\int _{0}^{1}{\frac {dx}{1+x^{2}}}\\&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta \,d\theta }{1+\tan ^{2}\theta }}\\&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta \,d\theta }{\sec ^{2}\theta }}\\&=4\int _{0}^{\pi /4}d\theta \\&=(4\theta ){\Bigg |}_{0}^{\pi /4}=4\left({\frac {\pi }{4}}-0\right)=\pi .\end{aligned}}

Meanwhile, direct application of the boundary terms to the formula for the antiderivative yields

∫ 0 1 4 d x 1 + x 2 = 4 ∫ 0 1 d x 1 + x 2 = 4 0 1 = 4 ( arctan ⁡ x ) | 0 1 = 4 ( arctan ⁡ 1 − arctan ⁡ 0 ) = 4 ( π 4 − 0 ) = π , {\displaystyle {\begin{aligned}\int _{0}^{1}{\frac {4\,dx}{1+x^{2}}}\,&=4\int _{0}^{1}{\frac {dx}{1+x^{2}}}\\&=4\left_{0}^{1}\\&=4(\arctan x){\Bigg |}_{0}^{1}\\&=4(\arctan 1-\arctan 0)\\&=4\left({\frac {\pi }{4}}-0\right)=\pi ,\end{aligned}}}

{\begin{aligned}\int _{0}^{1}{\frac {4\,dx}{1+x^{2}}}\,&=4\int _{0}^{1}{\frac {dx}{1+x^{2}}}\\&=4\left_{0}^{1}\\&=4(\arctan x){\Bigg |}_{0}^{1}\\&=4(\arctan 1-\arctan 0)\\&=4\left({\frac {\pi }{4}}-0\right)=\pi ,\end{aligned}}

same as before. Example 2

The integral

∫ a 2 + x 2 d x {\displaystyle \int {\sqrt {a^{2}+x^{2}}}\,{dx}} $\int {\sqrt {a^{2}+x^{2}}}\,{dx}$

may be evaluated by letting x = a tan ⁡ θ , d x = a sec 2 ⁡ θ d θ , θ = arctan ⁡ x a , {\displaystyle x=a\tan \theta ,\,dx=a\sec ^{2}\theta \,d\theta ,\,\theta =\arctan {\frac {x}{a}},} $x=a\tan \theta ,\,dx=a\sec ^{2}\theta \,d\theta ,\,\theta =\arctan {\frac {x}{a}},$

where a > 0 {\displaystyle a>0} $a>0$ so that a 2 = a , {\displaystyle {\sqrt {a^{2}}}=a,} ${\sqrt {a^{2}}}=a,$ and − π 2 < θ < π 2 {\displaystyle -{\frac {\pi }{2}}<\theta <{\frac {\pi }{2}}} $-{\frac {\pi }{2}}<\theta <{\frac {\pi }{2}}$ by the range of arctangent, so that sec ⁡ θ > 0 {\displaystyle \sec \theta >0} $\sec \theta >0$ and sec 2 ⁡ θ = sec ⁡ θ . {\displaystyle {\sqrt {\sec ^{2}\theta }}=\sec \theta .} ${\sqrt {\sec ^{2}\theta }}=\sec \theta .$

Then,

∫ a 2 + x 2 d x = ∫ a 2 + a 2 tan 2 ⁡ θ ( a sec 2 ⁡ θ ) d θ = ∫ a 2 ( 1 + tan 2 ⁡ θ ) ( a sec 2 ⁡ θ ) d θ = ∫ a 2 sec 2 ⁡ θ ( a sec 2 ⁡ θ ) d θ = ∫ ( a sec ⁡ θ ) ( a sec 2 ⁡ θ ) d θ = a 2 ∫ sec 3 ⁡ θ d θ . {\displaystyle {\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&=\int {\sqrt {a^{2}+a^{2}\tan ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\&=\int {\sqrt {a^{2}(1+\tan ^{2}\theta )}}\,(a\sec ^{2}\theta )\,d\theta \\&=\int {\sqrt {a^{2}\sec ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\&=\int (a\sec \theta )(a\sec ^{2}\theta )\,d\theta \\&=a^{2}\int \sec ^{3}\theta \,d\theta .\\\end{aligned}}}

{\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&=\int {\sqrt {a^{2}+a^{2}\tan ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\&=\int {\sqrt {a^{2}(1+\tan ^{2}\theta )}}\,(a\sec ^{2}\theta )\,d\theta \\&=\int {\sqrt {a^{2}\sec ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\&=\int (a\sec \theta )(a\sec ^{2}\theta )\,d\theta \\&=a^{2}\int \sec ^{3}\theta \,d\theta .\\\end{aligned}}

The integral of secant cubed may be evaluated using integration by parts. As a result, ∫ a 2 + x 2 d x = a 2 2 ( sec ⁡ θ tan ⁡ θ + ln ⁡ | sec ⁡ θ + tan ⁡ θ | ) + C = a 2 2 ( 1 + x 2 a 2 ⋅ x a + ln ⁡ | 1 + x 2 a 2 + x a | ) + C = 1 2 ( x a 2 + x 2 + a 2 ln ⁡ | x + a 2 + x 2 a | ) + C . {\displaystyle {\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)+C\\&={\frac {a^{2}}{2}}\left({\sqrt {1+{\frac {x^{2}}{a^{2}}}}}\cdot {\frac {x}{a}}+\ln \left|{\sqrt {1+{\frac {x^{2}}{a^{2}}}}}+{\frac {x}{a}}\right|\right)+C\\&={\frac {1}{2}}\left(x{\sqrt {a^{2}+x^{2}}}+a^{2}\ln \left|{\frac {x+{\sqrt {a^{2}+x^{2}}}}{a}}\right|\right)+C.\end{aligned}}}

{\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)+C\\&={\frac {a^{2}}{2}}\left({\sqrt {1+{\frac {x^{2}}{a^{2}}}}}\cdot {\frac {x}{a}}+\ln \left|{\sqrt {1+{\frac {x^{2}}{a^{2}}}}}+{\frac {x}{a}}\right|\right)+C\\&={\frac {1}{2}}\left(x{\sqrt {a^{2}+x^{2}}}+a^{2}\ln \left|{\frac {x+{\sqrt {a^{2}+x^{2}}}}{a}}\right|\right)+C.\end{aligned}}

Case III: Integrands containing x2 − a2

Let x = a sec ⁡ θ , {\displaystyle x=a\sec \theta ,} $x=a\sec \theta ,$ and use the identity sec 2 ⁡ θ − 1 = tan 2 ⁡ θ . {\displaystyle \sec ^{2}\theta -1=\tan ^{2}\theta .} $\sec ^{2}\theta -1=\tan ^{2}\theta .$

Examples of Case III

Geometric construction for Case III

Integrals such as

∫ d x x 2 − a 2 {\displaystyle \int {\frac {dx}{x^{2}-a^{2}}}} $\int {\frac {dx}{x^{2}-a^{2}}}$

can also be evaluated by partial fractions rather than trigonometric substitutions. However, the integral

∫ x 2 − a 2 d x {\displaystyle \int {\sqrt {x^{2}-a^{2}}}\,dx} $\int {\sqrt {x^{2}-a^{2}}}\,dx$

cannot. In this case, an appropriate substitution is:

x = a sec ⁡ θ , d x = a sec ⁡ θ tan ⁡ θ d θ , θ = arcsec ⁡ x a , {\displaystyle x=a\sec \theta ,\,dx=a\sec \theta \tan \theta \,d\theta ,\,\theta =\operatorname {arcsec} {\frac {x}{a}},}

x=a\sec \theta ,\,dx=a\sec \theta \tan \theta \,d\theta ,\,\theta =\operatorname {arcsec} {\frac {x}{a}},

where a > 0 {\displaystyle a>0} $a>0$ so that a 2 = a , {\displaystyle {\sqrt {a^{2}}}=a,} ${\sqrt {a^{2}}}=a,$ and 0 ≤ θ < π 2 {\displaystyle 0\leq \theta <{\frac {\pi }{2}}} $0\leq \theta <{\frac {\pi }{2}}$ by assuming x > 0 , {\displaystyle x>0,} $x>0,$ so that tan ⁡ θ ≥ 0 {\displaystyle \tan \theta \geq 0} $\tan \theta \geq 0$ and tan 2 ⁡ θ = tan ⁡ θ . {\displaystyle {\sqrt {\tan ^{2}\theta }}=\tan \theta .} ${\sqrt {\tan ^{2}\theta }}=\tan \theta .$

Then,

∫ x 2 − a 2 d x = ∫ a 2 sec 2 ⁡ θ − a 2 ⋅ a sec ⁡ θ tan ⁡ θ d θ = ∫ a 2 ( sec 2 ⁡ θ − 1 ) ⋅ a sec ⁡ θ tan ⁡ θ d θ = ∫ a 2 tan 2 ⁡ θ ⋅ a sec ⁡ θ tan ⁡ θ d θ = ∫ a 2 sec ⁡ θ tan 2 ⁡ θ d θ = a 2 ∫ ( sec ⁡ θ ) ( sec 2 ⁡ θ − 1 ) d θ = a 2 ∫ ( sec 3 ⁡ θ − sec ⁡ θ ) d θ . {\displaystyle {\begin{aligned}\int {\sqrt {x^{2}-a^{2}}}\,dx&=\int {\sqrt {a^{2}\sec ^{2}\theta -a^{2}}}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int {\sqrt {a^{2}(\sec ^{2}\theta -1)}}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int {\sqrt {a^{2}\tan ^{2}\theta }}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int a^{2}\sec \theta \tan ^{2}\theta \,d\theta \\&=a^{2}\int (\sec \theta )(\sec ^{2}\theta -1)\,d\theta \\&=a^{2}\int (\sec ^{3}\theta -\sec \theta )\,d\theta .\end{aligned}}}

{\begin{aligned}\int {\sqrt {x^{2}-a^{2}}}\,dx&=\int {\sqrt {a^{2}\sec ^{2}\theta -a^{2}}}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int {\sqrt {a^{2}(\sec ^{2}\theta -1)}}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int {\sqrt {a^{2}\tan ^{2}\theta }}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int a^{2}\sec \theta \tan ^{2}\theta \,d\theta \\&=a^{2}\int (\sec \theta )(\sec ^{2}\theta -1)\,d\theta \\&=a^{2}\int (\sec ^{3}\theta -\sec \theta )\,d\theta .\end{aligned}}

One may evaluate the integral of the secant function by multiplying the numerator and denominator by ( sec ⁡ θ + tan ⁡ θ ) {\displaystyle (\sec \theta +\tan \theta )} $(\sec \theta +\tan \theta )$ and the integral of secant cubed by parts. As a result,

∫ x 2 − a 2 d x = a 2 2 ( sec ⁡ θ tan ⁡ θ + ln ⁡ | sec ⁡ θ + tan ⁡ θ | ) − a 2 ln ⁡ | sec ⁡ θ + tan ⁡ θ | + C = a 2 2 ( sec ⁡ θ tan ⁡ θ − ln ⁡ | sec ⁡ θ + tan ⁡ θ | ) + C = a 2 2 ( x a ⋅ x 2 a 2 − 1 − ln ⁡ | x a + x 2 a 2 − 1 | ) + C = 1 2 ( x x 2 − a 2 − a 2 ln ⁡ | x + x 2 − a 2 a | ) + C . {\displaystyle {\begin{aligned}\int {\sqrt {x^{2}-a^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)-a^{2}\ln |\sec \theta +\tan \theta |+C\\&={\frac {a^{2}}{2}}(\sec \theta \tan \theta -\ln |\sec \theta +\tan \theta |)+C\\&={\frac {a^{2}}{2}}\left({\frac {x}{a}}\cdot {\sqrt {{\frac {x^{2}}{a^{2}}}-1}}-\ln \left|{\frac {x}{a}}+{\sqrt {{\frac {x^{2}}{a^{2}}}-1}}\right|\right)+C\\&={\frac {1}{2}}\left(x{\sqrt {x^{2}-a^{2}}}-a^{2}\ln \left|{\frac {x+{\sqrt {x^{2}-a^{2}}}}{a}}\right|\right)+C.\end{aligned}}}

{\begin{aligned}\int {\sqrt {x^{2}-a^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)-a^{2}\ln |\sec \theta +\tan \theta |+C\\&={\frac {a^{2}}{2}}(\sec \theta \tan \theta -\ln |\sec \theta +\tan \theta |)+C\\&={\frac {a^{2}}{2}}\left({\frac {x}{a}}\cdot {\sqrt {{\frac {x^{2}}{a^{2}}}-1}}-\ln \left|{\frac {x}{a}}+{\sqrt {{\frac {x^{2}}{a^{2}}}-1}}\right|\right)+C\\&={\frac {1}{2}}\left(x{\sqrt {x^{2}-a^{2}}}-a^{2}\ln \left|{\frac {x+{\sqrt {x^{2}-a^{2}}}}{a}}\right|\right)+C.\end{aligned}}

When π 2 < θ ≤ π , {\displaystyle {\frac {\pi }{2}}<\theta \leq \pi ,} ${\frac {\pi }{2}}<\theta \leq \pi ,$ which happens when x < 0 {\displaystyle x<0} $x<0$ given the range of arcsecant, tan ⁡ θ ≤ 0 , {\displaystyle \tan \theta \leq 0,} $\tan \theta \leq 0,$ meaning tan 2 ⁡ θ = − tan ⁡ θ {\displaystyle {\sqrt {\tan ^{2}\theta }}=-\tan \theta } ${\sqrt {\tan ^{2}\theta }}=-\tan \theta$ instead in that case.

Substitutions that eliminate trigonometric functions

Substitution can be used to remove trigonometric functions.

For instance,

∫ f ( sin ⁡ ( x ) , cos ⁡ ( x ) ) d x = ∫ 1 ± 1 − u 2 f ( u , ± 1 − u 2 ) d u u = sin ⁡ ( x ) ∫ f ( sin ⁡ ( x ) , cos ⁡ ( x ) ) d x = ∫ 1 ∓ 1 − u 2 f ( ± 1 − u 2 , u ) d u u = cos ⁡ ( x ) ∫ f ( sin ⁡ ( x ) , cos ⁡ ( x ) ) d x = ∫ 2 1 + u 2 f ( 2 u 1 + u 2 , 1 − u 2 1 + u 2 ) d u u = tan ⁡ ( x 2 ) {\displaystyle {\begin{aligned}\int f(\sin(x),\cos(x))\,dx&=\int {\frac {1}{\pm {\sqrt {1-u^{2}}}}}f\left(u,\pm {\sqrt {1-u^{2}}}\right)\,du&&u=\sin(x)\\\int f(\sin(x),\cos(x))\,dx&=\int {\frac {1}{\mp {\sqrt {1-u^{2}}}}}f\left(\pm {\sqrt {1-u^{2}}},u\right)\,du&&u=\cos(x)\\\int f(\sin(x),\cos(x))\,dx&=\int {\frac {2}{1+u^{2}}}f\left({\frac {2u}{1+u^{2}}},{\frac {1-u^{2}}{1+u^{2}}}\right)\,du&&u=\tan \left({\tfrac {x}{2}}\right)\\\end{aligned}}} ${\begin{aligned}\int f(\sin(x),\cos(x))\,dx&=\int {\frac {1}{\pm {\sqrt {1-u^{2}}}}}f\left(u,\pm {\sqrt {1-u^{2}}}\right)\,du&&u=\sin(x)\\\int f(\sin(x),\cos(x))\,dx&=\int {\frac {1}{\mp {\sqrt {1-u^{2}}}}}f\left(\pm {\sqrt {1-u^{2}}},u\right)\,du&&u=\cos(x)\\\int f(\sin(x),\cos(x))\,dx&=\int {\frac {2}{1+u^{2}}}f\left({\frac {2u}{1+u^{2}}},{\frac {1-u^{2}}{1+u^{2}}}\right)\,du&&u=\tan \left({\tfrac {x}{2}}\right)\\\end{aligned}}$

The last substitution is known as the Weierstrass substitution, which makes use of tangent half-angle formulas.

For example,

∫ 4 cos ⁡ x ( 1 + cos ⁡ x ) 3 d x = ∫ 2 1 + u 2 4 ( 1 − u 2 1 + u 2 ) ( 1 + 1 − u 2 1 + u 2 ) 3 d u = ∫ ( 1 − u 2 ) ( 1 + u 2 ) d u = ∫ ( 1 − u 4 ) d u = u − u 5 5 + C = tan ⁡ x 2 − 1 5 tan 5 ⁡ x 2 + C . {\displaystyle {\begin{aligned}\int {\frac {4\cos x}{(1+\cos x)^{3}}}\,dx&=\int {\frac {2}{1+u^{2}}}{\frac {4\left({\frac {1-u^{2}}{1+u^{2}}}\right)}{\left(1+{\frac {1-u^{2}}{1+u^{2}}}\right)^{3}}}\,du=\int (1-u^{2})(1+u^{2})\,du\\&=\int (1-u^{4})\,du=u-{\frac {u^{5}}{5}}+C=\tan {\frac {x}{2}}-{\frac {1}{5}}\tan ^{5}{\frac {x}{2}}+C.\end{aligned}}} ${\begin{aligned}\int {\frac {4\cos x}{(1+\cos x)^{3}}}\,dx&=\int {\frac {2}{1+u^{2}}}{\frac {4\left({\frac {1-u^{2}}{1+u^{2}}}\right)}{\left(1+{\frac {1-u^{2}}{1+u^{2}}}\right)^{3}}}\,du=\int (1-u^{2})(1+u^{2})\,du\\&=\int (1-u^{4})\,du=u-{\frac {u^{5}}{5}}+C=\tan {\frac {x}{2}}-{\frac {1}{5}}\tan ^{5}{\frac {x}{2}}+C.\end{aligned}}$

Hyperbolic substitution

Substitutions of hyperbolic functions can also be used to simplify integrals.

In the integral ∫ d x a 2 + x 2 , {\displaystyle \int {\frac {dx}{\sqrt {a^{2}+x^{2}}}}\,,} $\int {\frac {dx}{\sqrt {a^{2}+x^{2}}}}\,,$ make the substitution x = a sinh ⁡ u , {\displaystyle x=a\sinh {u},} $x=a\sinh {u},$ d x = a cosh ⁡ u d u . {\displaystyle dx=a\cosh u\,du.} $dx=a\cosh u\,du.$

Then, using the identities cosh 2 ⁡ ( x ) − sinh 2 ⁡ ( x ) = 1 {\displaystyle \cosh ^{2}(x)-\sinh ^{2}(x)=1} $\cosh ^{2}(x)-\sinh ^{2}(x)=1$ and sinh − 1 ⁡ x = ln ⁡ ( x + x 2 + 1 ) , {\displaystyle \sinh ^{-1}{x}=\ln(x+{\sqrt {x^{2}+1}}),} $\sinh ^{-1}{x}=\ln(x+{\sqrt {x^{2}+1}}),$

∫ d x a 2 + x 2 = ∫ a cosh ⁡ u d u a 2 + a 2 sinh 2 ⁡ u , = ∫ a cosh ⁡ u d u a 1 + sinh 2 ⁡ u = ∫ a cosh ⁡ u a cosh ⁡ u d u = u + C = sinh − 1 ⁡ x a + C = ln ⁡ ( x 2 a 2 + 1 + x a ) + C = ln ⁡ ( x 2 + a 2 + x a ) + C {\displaystyle {\begin{aligned}\int {\frac {dx}{\sqrt {a^{2}+x^{2}}}}\,&=\int {\frac {a\cosh u\,du}{\sqrt {a^{2}+a^{2}\sinh ^{2}u}}}\ ,\\&=\int {\frac {a\cosh {u}\,du}{a{\sqrt {1+\sinh ^{2}{u}}}}}\,\\&=\int {\frac {a\cosh {u}}{a\cosh u}}\,du\\&=u+C\\&=\sinh ^{-1}{\frac {x}{a}}+C\\&=\ln \left({\sqrt {{\frac {x^{2}}{a^{2}}}+1}}+{\frac {x}{a}}\right)+C\\&=\ln \left({\frac {{\sqrt {x^{2}+a^{2}}}+x}{a}}\right)+C\end{aligned}}} ${\begin{aligned}\int {\frac {dx}{\sqrt {a^{2}+x^{2}}}}\,&=\int {\frac {a\cosh u\,du}{\sqrt {a^{2}+a^{2}\sinh ^{2}u}}}\ ,\\&=\int {\frac {a\cosh {u}\,du}{a{\sqrt {1+\sinh ^{2}{u}}}}}\,\\&=\int {\frac {a\cosh {u}}{a\cosh u}}\,du\\&=u+C\\&=\sinh ^{-1}{\frac {x}{a}}+C\\&=\ln \left({\sqrt {{\frac {x^{2}}{a^{2}}}+1}}+{\frac {x}{a}}\right)+C\\&=\ln \left({\frac {{\sqrt {x^{2}+a^{2}}}+x}{a}}\right)+C\end{aligned}}$

References

^ Stewart, James (2008). Calculus: Early Transcendentals (6th ed.). Brooks/Cole. ISBN 978-0-495-01166-8.
^ Thomas, George B.; Weir, Maurice D.; Hass, Joel (2010). Thomas' Calculus: Early Transcendentals (12th ed.). Addison-Wesley. ISBN 978-0-321-58876-0.
^ Stewart, James (2012). "Section 7.2: Trigonometric Integrals". Calculus - Early Transcendentals. United States: Cengage Learning. pp. 475–6. ISBN 978-0-538-49790-9.
^ Boyadzhiev, Khristo N. "Hyperbolic Substitutions for Integrals" (PDF). Archived from the original (PDF) on 26 February 2020. Retrieved 4 March 2013.

v t e Integrals
Types of integrals	Riemann integral Lebesgue integral Burkill integral Bochner integral Daniell integral Darboux integral Henstock–Kurzweil integral Haar integral Hellinger integral Khinchin integral Kolmogorov integral Lebesgue–Stieltjes integral Pettis integral Pfeffer integral Riemann–Stieltjes integral Regulated integral
Integration techniques	Substitution Trigonometric Euler Weierstrass By parts Partial fractions Euler's formula Inverse functions Changing order Reduction formulas Parametric derivatives Differentiation under the integral sign Laplace transform Contour integration Laplace's method Numerical integration Simpson's rule Trapezoidal rule Risch algorithm
Improper integrals	Gaussian integral Dirichlet integral Fermi–Dirac integral complete incomplete Bose–Einstein integral Frullani integral Common integrals in quantum field theory
Stochastic integrals	Itô integral Russo–Vallois integral Stratonovich integral Skorokhod integral
Miscellaneous	Basel problem Euler–Maclaurin formula Gabriel's horn Integration Bee Proof that 22/7 exceeds π Volumes Washers Shells

Trigonometric substitution

Case I: Integrands containing a2 − x2

Examples of Case I

Case II: Integrands containing a2 + x2

Examples of Case II

Case III: Integrands containing x2 − a2

Examples of Case III

Substitutions that eliminate trigonometric functions

Hyperbolic substitution

See also

References